鏡頭的分辨率
來(lái)源:深圳市凱茉銳電子科技有限公司2024-12-13
鏡頭的分辨率
描述鏡頭成像質(zhì)量的內(nèi)在指標(biāo)是鏡頭的光學(xué)傳遞函數(shù)與畸變,但對(duì)擁護(hù)而言,需要了解的僅僅是鏡頭的空間分辨率,以每毫米能夠分辨的黑白條紋線對(duì)為計(jì)量單位,計(jì)算公式為:鏡頭分辨率N=視野總線數(shù)/2/畫幅格式(L/W)。如500W像素鏡頭,2/3’傳感器,則有2448/2/8.8=139線對(duì)/毫米。
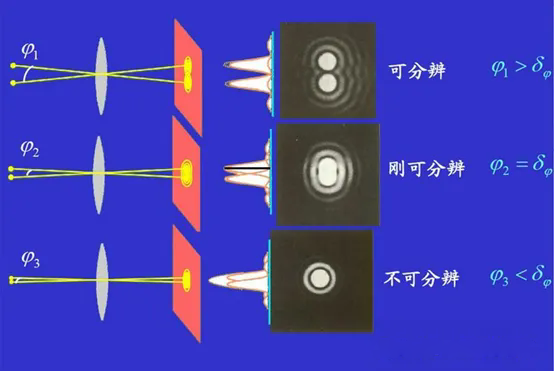
光學(xué)儀器形成分立圖像能力的定量度量,又稱分辨率。由于鏡頭(光瞳)對(duì)光束的限制而產(chǎn)生的衍射效應(yīng),使物點(diǎn)發(fā)射的光波在像面上不可能成為一個(gè)像點(diǎn),而是以像點(diǎn)為中心擴(kuò)展為一定的強(qiáng)度分布,其中心斑就是夫瑯和費(fèi)衍射的零級(jí)斑,也叫做愛(ài)里斑。這就是說(shuō),即使不考慮所有幾何像差,成像光學(xué)儀器也無(wú)法實(shí)現(xiàn)點(diǎn)物成點(diǎn)像的理想情況。因此,物面上相距很近的兩個(gè)分離的物點(diǎn),在像面上就可能成為兩個(gè)互相重疊的衍射斑,這兩個(gè)衍射斑甚至可能過(guò)度重疊,變得模糊一團(tuán),以致觀察者無(wú)法辨認(rèn)物方兩個(gè)物點(diǎn)的存在。總之,物方圖像是大量物點(diǎn)的集合,而變換到像面上的強(qiáng)度分布卻是大量衍射斑的集合,它不可能準(zhǔn)確地反映物面上的所有細(xì)節(jié)。為了給光學(xué)儀器規(guī)定一個(gè)分辨細(xì)節(jié)能力的統(tǒng)一標(biāo)準(zhǔn),通常采用瑞利判據(jù)。瑞利判據(jù)規(guī)定,當(dāng)一個(gè)像斑中心剛好落在另一個(gè)像斑邊緣(即一級(jí)暗環(huán))時(shí),確認(rèn)兩個(gè)像斑剛剛可以分辨(見(jiàn)圖b)。計(jì)算表明,滿足瑞利判據(jù)時(shí)的兩個(gè)像斑強(qiáng)度的不相干疊加的結(jié)果,其光強(qiáng)起伏量約為20%,正常人眼是能分辨這種光強(qiáng)差別的。當(dāng)然對(duì)于客觀的光接收器如乳膠底片、光電管之類,或其他傳感器來(lái)說(shuō),也許并不苛求20%的起伏量作為它的可分辨的界限,但瑞利判據(jù)仍然可作為一個(gè)相對(duì)標(biāo)準(zhǔn),用以估算和比較光學(xué)儀器的分辨本領(lǐng)。
分辨本領(lǐng)
人眼眼瞳的直徑De可在2~8mm范圍內(nèi)調(diào)節(jié)。根據(jù)瑞利判據(jù),并由愛(ài)里斑的半角寬度公式,可以求得人眼的最小分辨角公式為δθe=1.22λ/ De
以De=2mm,光波長(zhǎng)λ=0.55μm估算,人眼的最小分辨角數(shù)值為3.355*10^-4弧度(弧度=角度/180°*PI)δθe≈1’=0.075mm/25cm=3mm/10m
即正常人能分辨明視距離25cm處相隔0.075mm的兩條刻線,或者說(shuō),能分辨10m遠(yuǎn)處相隔3mm的兩條刻線。生理光學(xué)的這一數(shù)據(jù)對(duì)于助視光學(xué)儀器和電視機(jī)的設(shè)計(jì),以及對(duì)于圖像識(shí)別這類問(wèn)題,都是必須考慮的基本數(shù)據(jù)。
望遠(yuǎn)鏡
它觀察的對(duì)象是遠(yuǎn)物,其本身線度并不小,故通常以最小分辨角δθm直接標(biāo)志它的分辨本領(lǐng)。望遠(yuǎn)鏡的最小分辨角公式為
δθm≈1.22λ/D(弧度)
式中λ為媒質(zhì)中的光波長(zhǎng),D為光瞳(物鏡)的直徑。以D=2000mm,λ=0.55μm估算,δθm≈0.06″。為減少δθm以提高分辨本領(lǐng),必須加大物鏡口徑。由于光波在長(zhǎng)程傳輸過(guò)程中受大氣擾動(dòng)的影響,天文望遠(yuǎn)鏡的實(shí)際分辨本領(lǐng)比上述理論分辨本領(lǐng)要低。因此,每個(gè)國(guó)家都盡可能地將大型的天文望遠(yuǎn)鏡設(shè)在高山頂上。中國(guó)云南天文臺(tái)設(shè)在海拔 2300m的山頂上。美國(guó)于1981年在夏威夷建成的一臺(tái)紅外望遠(yuǎn)鏡,直徑為3357mm,設(shè)在海拔4200m的山頂上,它可觀測(cè)幾十億光年遠(yuǎn)的天體,用來(lái)研究一般光學(xué)望遠(yuǎn)鏡不易觀測(cè)的天體的分子結(jié)構(gòu)和正在形成過(guò)程中的星體外殼。
顯微鏡
它的觀察對(duì)象是細(xì)小的近物,故通常以最小分辨距離δym直接標(biāo)志它的分辨本領(lǐng)。根據(jù)瑞利判據(jù)以及愛(ài)里斑的半角寬度公式,并考慮到顯微鏡工作在齊明點(diǎn),可以導(dǎo)出顯微鏡的最小分辨距離公式為
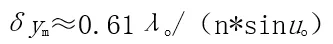
式中n為物方折射率,uo為物光束的孔徑角,λo為真空波長(zhǎng),乘積n*sinuo稱為數(shù)值孔徑,用N.A.表示。作為一種數(shù)量級(jí)的估算,數(shù)值孔徑最大不超過(guò)N.A.≈n≈1.5(油浸鏡頭),故δym有個(gè)限度
δym≥0.4λo,
在可見(jiàn)光波段, δym≥0.2μm。為了充分發(fā)揮顯微鏡的分辨能力,應(yīng)將δym放大到足以使眼睛可分辨的距離δye≈δθe×25cm≈0.075mm,由此估算光學(xué)顯微鏡的橫向線放大率v≈δye/δym≈400倍。當(dāng)然過(guò)高的放大率也沒(méi)有必要,此時(shí)儀器仍然無(wú)法分辨δym以下的細(xì)節(jié)。這個(gè)與分辨本領(lǐng)相匹配的放大率稱為顯微鏡的正常放大率或有效放大率。設(shè)計(jì)時(shí)一般選用放大率稍大于正常放大率,光學(xué)顯微鏡的放大率不超過(guò)1000倍。進(jìn)一步提高顯微鏡分辨本領(lǐng)的惟一途徑是縮短波長(zhǎng)。近代電子顯微鏡利用電子束的波動(dòng)性經(jīng)“磁透鏡”成像,電子束的波長(zhǎng)很短(取決于加速電壓),可達(dá)┱量級(jí),不過(guò)電子束的孔徑角也小(不到10°),其結(jié)果可使電子顯微鏡的分辨本領(lǐng)比光學(xué)顯微鏡的高幾個(gè)數(shù)量級(jí),相應(yīng)的放大率可達(dá)數(shù)萬(wàn)倍至百萬(wàn)倍,能顯示蛋白質(zhì)分子結(jié)構(gòu)。
攝影系統(tǒng)
攝影系統(tǒng)(如照相機(jī)、電視攝像機(jī)一類)一般工作于遠(yuǎn)物短焦距情形,它與助視光學(xué)儀器(望遠(yuǎn)鏡、顯微鏡)不同之點(diǎn)在于,物經(jīng)攝影鏡頭成為一個(gè)縮小的實(shí)像被感光介質(zhì)直接記錄。因此,在分析整個(gè)系統(tǒng)的分辨本領(lǐng)問(wèn)題時(shí),既要考慮到鏡頭(光瞳)的衍射效應(yīng),又要考慮到記錄介質(zhì)本身的空間分辨率N──感光乳劑單位長(zhǎng)度內(nèi)能分辨的線紋數(shù)目。鏡頭衍射效應(yīng)限制的物方最小分辨角公式仍然是δθe=1.22λ/ D,在像面上的攝影系統(tǒng)的最小分辨線度相應(yīng)地為δy’m≈1.22λf/D,式中f為鏡頭焦距,比值D/f稱為鏡頭的相對(duì)孔徑。相對(duì)孔徑越大,則鏡頭的分辨本領(lǐng)越高。以相對(duì)孔徑1∶3.5估算,δy’m ≈2.35 μm。為了充分利用鏡頭的分辨本領(lǐng),記錄介質(zhì)的分辨率應(yīng)滿足N≥1/δy╭≈425mm^-1,即要求選用每毫米能分開(kāi)425條線紋以上的感光乳劑。
以上給出的光學(xué)成像儀器的分辨本領(lǐng)的公式是僅考慮衍射效應(yīng)以后的理論公式,而實(shí)際上成像儀器還有各種各樣的幾何像差,對(duì)攝影系統(tǒng)尤其如此,所以儀器的實(shí)際分辨本領(lǐng)比理論值要低一些,有些甚至降低一個(gè)量級(jí)。將破壞點(diǎn)物成點(diǎn)像的各種因素綜合起來(lái),統(tǒng)一地對(duì)成像質(zhì)量作出評(píng)價(jià)的工作開(kāi)始于20世紀(jì)50年代興起的光學(xué)傳遞函數(shù)的概念。
相關(guān)資訊
基礎(chǔ)知識(shí)之?dāng)?shù)字圖像處理
2025-03-07- 2025-03-06
- 2025-03-05
工業(yè)相機(jī)選型:如何選擇最適合的相機(jī)?
2025-03-04- 2025-03-03
機(jī)器視覺(jué)相機(jī)、鏡頭選型詳細(xì)流程
2025-02-28





 13798538021
13798538021